CSAPP学习笔记(1)
CSAPP学习笔记(1)
前言
在开始这篇学习笔记之前,笔者先叠个甲(因为笔者感觉CSAPP这门课并不算很容易接受,虽然被普遍认为是计算机学科的基础)并且感觉这门课涉猎甚广多管闲事
另外,为什么计算机系统这门课被称为CSAPP呢,其实CSAPP的全称是ComputerSystem:A programer perspective (程序员视角下的计算机系统)虽然感觉大多数程序员并没有这个视角
闲话少说,开始追求力量
信息的储存
十六进制表示法
一个字节有8位,如果采用二进制来表示则过于冗长,如果使用十进制转化起来又十分麻烦,所以常用C语言中以0x开头来表示一个十六进制数,来表示16进制数值
寻址与储存
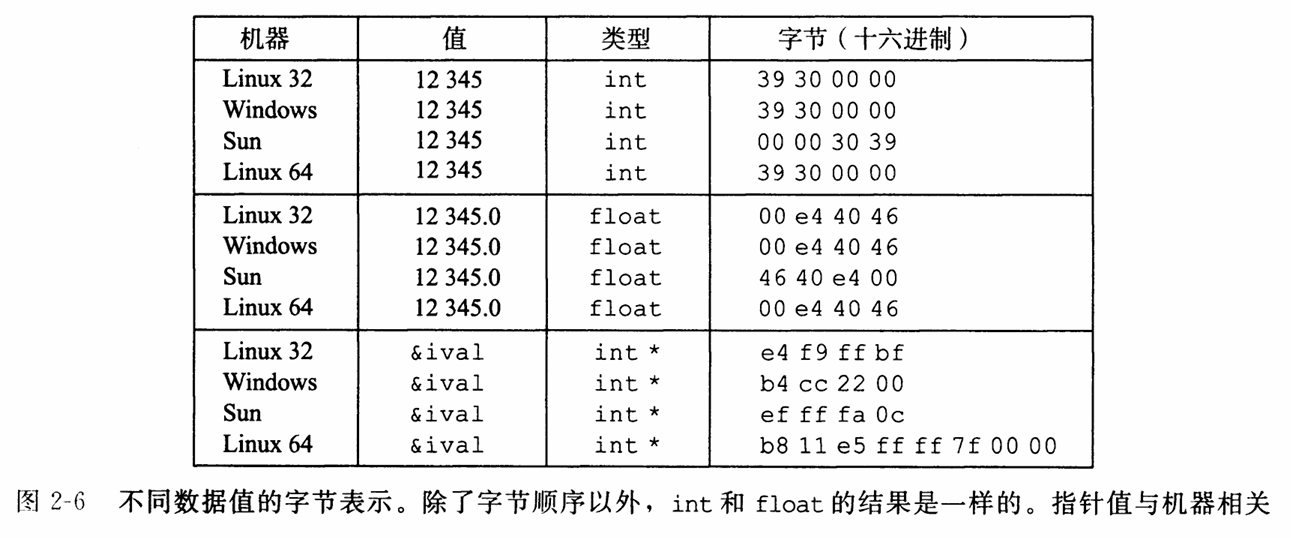
在几乎所有的机器上,多字节对象都被存储为连续的字节序列,对象的地址为所使用字节中最小的地址。
例如,假设一个类型为int的变量x的地址为0x100,也就是说,地址表达式&x的值为0x100那么, (假设数据类型int为32位表示)x的4个字节将被存储在内存的0x100、0x101、0x102和0x103位置
虽然位置相同,但存储的时候却有两种规则——大端法和小端法
- 最低有效字节在最前面的方式,称为小端法(little endian)。
- 最高有效字节在最前面的方式,称为大端法(big endian)
12345的十六进制表示为0x00003039,所以上图中Sun为大端法表示,其余为小端法。
C语言中的移位操作
众所周知,移位分为左移和右移。
左移的规则较为简单,仅需在右侧补0即可,这并不代表左移就不会出现错误,但这并不是位运算的问题,而是会溢出
而右移则会分为两种情况
- 逻辑右移:即简单的在左侧补0即可
- 算术右移:保留被移动数的最高有效位
为什么会有算数右移的存在,其实就是用于处理有符号数的移位后运算正确性,在补码表示的情况下,算术右移有奇效
不幸的是,C语言并没有规定有符号数的右移使用哪种右移,但是幸运的是,几乎所有的编译器/机器组合都使用了算术右移。对于无符号数,逻辑右移是必须的。
整数的编码方式
对于无符号数展开,仅需简单按位展开即可,这里不过多介绍
而对于有符号数的展开,计算机中常采用补码的方式进行储存,补码的计算其实同样也是按位展开,只不过累加时最高位的权重为负的2的幂次
有符号数和无符号数之间的转换
这里需要注意的点有两点,下面一一介绍
- 在有符号数和无符号数强制类型转换时,采用的规则是计算机并不会改变该数据的位,而是改变解释该数据的方式
若是在两者表示想通数值的范围内,则可以实现无痛转换,若是该位表示在两种编码方式内的值并不相通,则会改变该数值
例:-12345转化为无符号数则会被解释为53191(数据仅有16位)值得一提的是 12345+53191=65536=2^16 - 当一个有符号数和一个无符号数在同一个算术表达式中,则会均被转化为无符号数
浮点数
IEEE浮点表示
浮点数的计算公式如下
$$
V = (-1)^s \times M \times 2^E
$$
其中S为符号位,M为阶位 通常情况下是一个 1 ~ 2 二进制小数,少数情况下会是 0 ~ 1 的二进制小数 取决于规格化与否(待会就写),E代表阶码(可以是负数)
在 exp≠000…0 和 exp≠111…1 时,都是规范化的值,在这两种情况下,表示特殊的数值
我们的公式中的 E 是一个偏移的值 E=Exp−Bias,其中
- Exp: 是 exp 编码区域的无符号数值
- Bias:值为
$$
2^{k-1} - 1
$$
的偏移量,其中 k 是 exp 编码的位数,也就是说
- 单精度:127(Exp: 1…254, E: -126…127)
- 双精度:1023(Exp: 1…2046, E: -1022…1023)
举个栗子:
$$
15213_{10}=11101101101101_2=1.1101101101101_2 \times 2^{13}
$$
那么在这里 13 就是上述公式里的 E 这个 13 的来源便是 将 15213转化为二进制后,将小数点左移13位将其化为一个二进制小数,则后面乘的阶数便是13。
而1.的后续部分则是上述公式里的 M
从这个过程可以看出,在规格化的情况下,二进制小数总是以1.M的形式出现 所以本着能省一位是一位节约材料的原则,我们将1省略只储存小数点后的部分
所以该例的完整储存方式如下
1 | 0 10001100 11011011011010000000000 |
非规格数
从上面的过程,我们不太自然的能捕捉到非规格数的产生原因是什么
其实就是这个浮点数过小,我们在找1.M的1的时候右移的位数过多已经超过了该类型的总位数
此时,我们规定 exp为 00000000
根据上面的计算规则,00000000 代表 E=-127 但实际上 对于非规格数 E=-126
产生如下矛盾的原因就在于能省一位是一位消失的1,此时的小数部分是0.E的形式存在的
特殊值
还有一些我们约定俗称的特殊值,当 exp = 11111111 时会出现
我们规定(事实也不是我规定的)当exp = 11111111 且 frac = 00000…时 代表无穷大,由于符号位所以同时存在正无穷和负无穷
例如
$$
1.0/0.0 = -1.0/0.0 = +\infty ,\ 1.0/ -0.0 = -\infty
$$
而当 exp = 11111111 且 frac!= 00000… 时 代表NaN(Not a number)
参考文献(巨佬 Orz)