电磁场与电磁波学习笔记(1)

矢量分析

前言

课程总述

场（静态）-> 麦克斯韦方程组 -> 波（时变）

从麦克斯韦方程组 得到 波动方程

从数学角度 本门课程就是解 麦克斯韦方程组 波动方程

引入矢量的意义

1. 为复杂的物理现象提供紧凑的数学表达
2. 便于直观的想象和运算变换

三重积

1. 标量三重积：

$$
A \cdot (B \times C) = B \cdot (C \times A) = C \cdot (A \times B)
$$

显然，若三个矢量代表一个六面体的边，则标量三重积是它的体积。

2. 矢量三重积：

$$
A \times (B \times C) = (A \cdot C)B - (A \cdot B)C
$$

不满足结合律 但满足上述性质

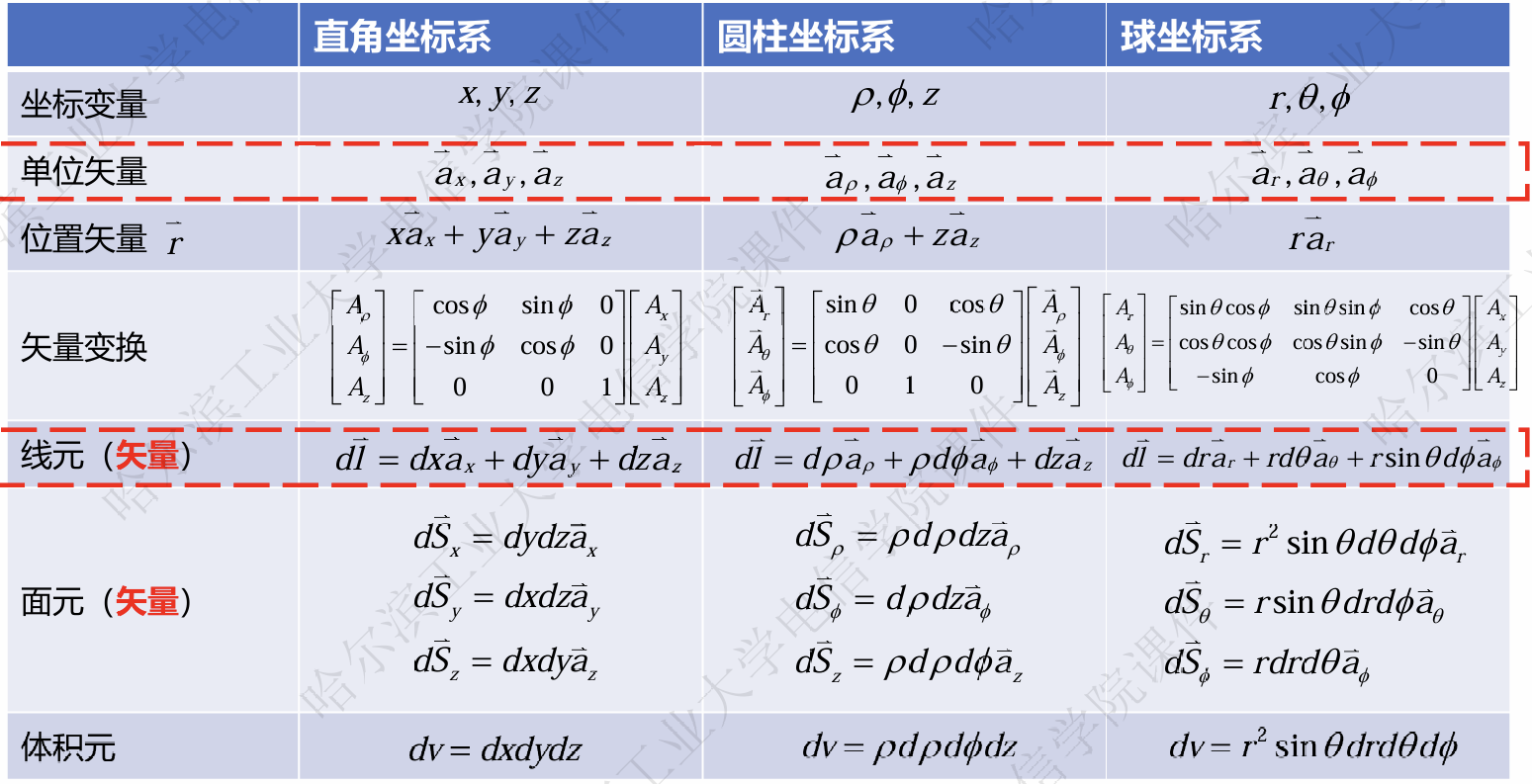
坐标系

矢量函数及其微分

在直角坐标下，

$$
\frac{\partial \mathbf{F}}{\partial x} = \frac{\partial}{\partial x} (\mathbf{a}_x F_x + \mathbf{a}_y F_y + \mathbf{a}_z F_z)
$$

$$
= \mathbf{a}_x \frac{\partial F_x}{\partial x} + F_x \frac{\partial \mathbf{a}_x}{\partial x} + \mathbf{a}_y \frac{\partial F_y}{\partial x} + F_y \frac{\partial \mathbf{a}_y}{\partial x} + \mathbf{a}_z \frac{\partial F_z}{\partial x} + F_z \frac{\partial \mathbf{a}_z}{\partial x}
$$

$$
= \mathbf{a}_x \frac{\partial F_x}{\partial x} + \mathbf{a}_y \frac{\partial F_y}{\partial x} + \mathbf{a}_z \frac{\partial F_z}{\partial x}
$$

由式可得结论，在直角坐标系中，矢量函数对某一坐标变量的偏导数(或导数）仍是一个矢量，它的各个分量等于原矢量函数各分量对该坐标变量的偏导数（或导数）。简单而言，只需把坐标单位矢量提到微分号外即可。但这里需注意的是，在柱坐标和球坐标系中，坐标单位矢量并非常矢量，故不能将其提到微分运算符号外，而需按照函数乘积的求导法则运算。

标量场的梯度

定义

场是某个物理量关于空间坐标（x,y,z）和时间（t）的函数

分类 ：

1. 标量场和矢量场
2. 静态场和动态场

标量场的等值线

概念: 场值相同的点在空间形成的曲面，叫等值面，在二位场中退化为等值线

方向导数

$$
\frac{\partial u}{\partial l} \bigg|{M_0} = \lim{\Delta l \to 0} \frac{u(M_0 + \Delta l) - u(M_0)}{\Delta l}
$$

直角坐标下的形式

$$
\frac{\partial u}{\partial l} = \frac{\partial u}{\partial x} \cos\alpha + \frac{\partial u}{\partial y} \cos\beta + \frac{\partial u}{\partial z} \cos\gamma
$$