存储器

存储器的校验

汉明码的组成

关于纠错理论的介绍，在此不多赘述。

假设需要检测的数据为n位，则我们需要添加的检验位的位数k需要满足下列公式，当理解了如何检验数据的过程后就能对这个公式有一定程度的理解。

$$
2^{k} \geq n + k + 1
$$

汉明码是如何检验的呢？我们直接从栗子开始看。

假设我们需要传输的数据为1011，根据上面的原理，我们需要三个校验位，我们将它们放在数据的1，2，4位上，分别叫做P1,P2,P3（现在不理解也没关系）

每个校验会负责不同位置的校验，在本例中 P1负责的是1 3 5 7号位置 P2负责2 3 6 7号位置 P3负责 4 5 6 7号位置 （现在不理解没关系）

通常采用偶校验的方式，我们先来介绍如何算出校验位

偶校验其实就是，检验位负责的各位置之和要为偶数 所以 对于P1 P1+1+0+1 为偶 所以 P1 = 0

同理 算出P2 = 1 P3 = 0 于是 我们完整的汉明码即为 0110011

假设我们 接受到的数据为 0110111 （第五位出错，我们仅考虑一位出错）

接收方如何发现第五位出错的呢？

检查校验位，P1负责的1357会变为奇数，P2的则不变，P3负责的 4567 也会变为奇数 我们检查出错区域的重合部分 即可发现是第五位出错

现在 你可能还有一些疑惑。到底是如何规定哪些校验位负责哪些区域的呢？如何保证出错区域的重合部分仅有一个数呢？

其实，校验位所负责的部分为 二进制数值编码中，所在编号位置为1的所有位置（先别骂不说人话）

举个栗子 仍是上述栗子 共有7位 可以用三位二进制数表示 0 0 0

则P1负责的位数为 所有第一位为1 的数 001 011 101 111 即1357

当 某一位出错的时候，所有出错的检验位在对应位数的值为1（先别骂不说人话）

仍然是上面的栗子 我们通过检查可以发现 P1和P3不满足偶校验原则，所以出错位的二进制数值在 第一位和第三位为1，其余位为0 所以其为101

至此 你已经理解了为什么要将P1 P2 P3 放在1 2 4号位置 （现在不理解有关系QAQ）

提高访存速度的策略

单体多字系统

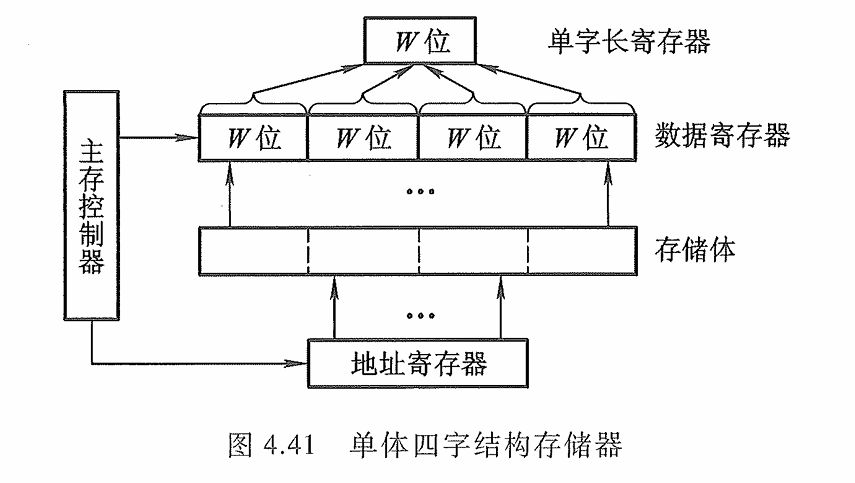
由于程序和数据在存储体内是连续存放的，因此 CPU 访存取出的信息也是连续的，如果可以在一个存取周期内，从同一地址取出 4条指令，然后再逐条将指令送至 CPU 执行，即每隔 1/4存取周期，主存向 CPU送一条指令，这样显然增大了存储器的带宽，提高了单体存储器的工作速度

图中示意了一个单体四字结构的存储器，每字 W位。按地址在一个存取周期内可读出 4xW位的指令或数据，使主存带宽提高到4倍。显然，采用这种办法的前提是：指令和数据在主存内必须是连续存放的，一旦遇到转移指令，或者操作数不能连续存放，这种方法的效果就不明显。

多体并行系统

多体并行系统就是采用多体模块组成的存储器。每个模块有相同的容量和存取速度，各模块各自都有独立的地址寄存器(MAR) 、数据寄存器(MDR)、地址译码、驱动电路和读／写电路，它们能并行工作，又能交叉工作。

高位交叉

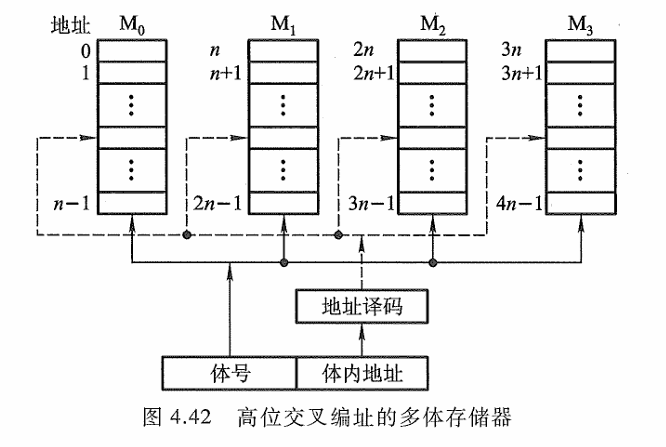
并行工作即同时访问 N个模块，同时启动，同时读出，完全并行地工作（不过，同时读出的 N个字在总线上需分时传送）。图4.42是适合于并行工作的高位交叉编址的多体存储器结构示意图，图中程序因按体内地址顺序存放（一个体存满后，再存入下一个体），故又有顺序存储之称。
显然，高位地址可表示体号，低位地址为体内地址。按这种编址方式，只要合理调动，使不同的请求源同时访问不同的体，便可实现并行工作。例如，当一个体正与 CPU交换信息时，另一个体可同时与外部设备进行直接存储器访问，实现两个体并行工作。这种编址方式由于一个体内的地址是连续的，有利于存储器的扩充。

高位交叉并不能提高性能。

低位交叉

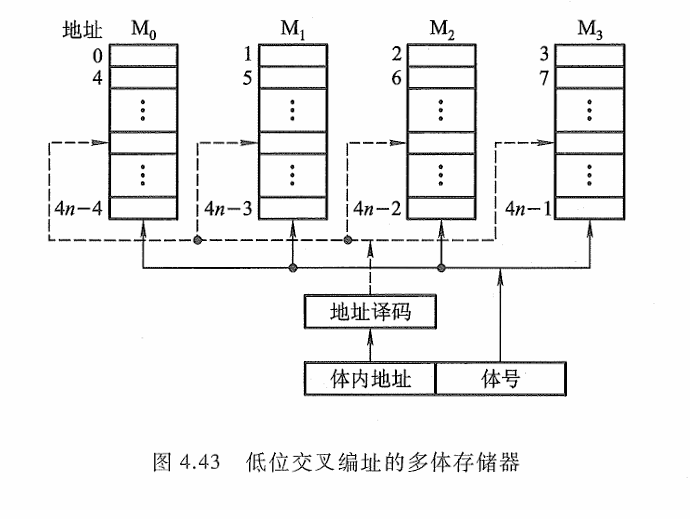
采用低位交叉的方式，连续的数据存在不同的存储器中。采用交叉编址的方式，显然低位地址用来表示体号，高位地址为体内地址。这种编址方法又称为模M编址(M等干模块数）

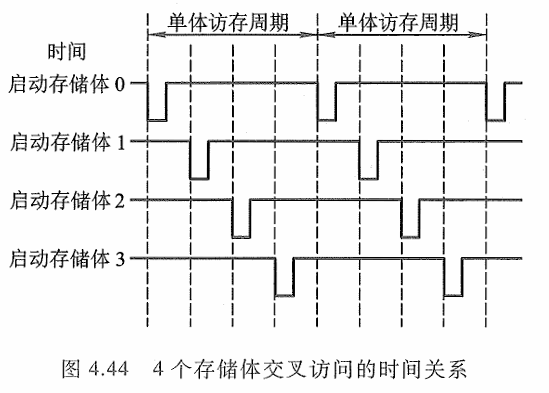
多体模块结构的存储器采用交叉编址后，可以在不改变每个模块存取周期的前提下，提高存储器的带宽。图4.44示意了CPU交叉访问4个存储体的时间关系，负脉冲为启动每个体的工作信号。虽然对每个体而言，存取周期均未缩短，但由于CPU交叉访问各体，使4个存储体的读／写过程重叠进行，最终在一个存取周期的时间内，存储器实际上向CPU提供了4个存储字。如果每个模块存储字长为32位，则在一个存取周期内（除第一个存取周期外），存储器向CPU提供了32x4=128位二进制代码，大大增加了存储器的带宽。

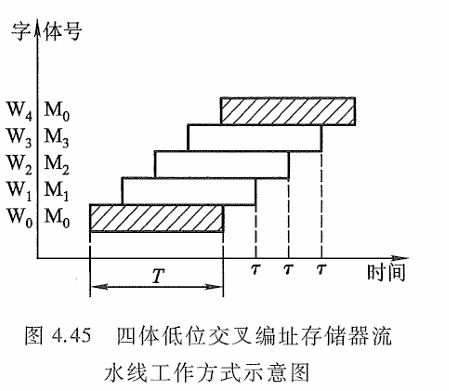
假设每个体的存储字长和数据总线的宽度一致，并假设低位交叉的存储器模块数为n，存取周期为T，总线传输周期为τ，那么当采用流水线方式（如图4.44所示）存取时，应满足T=nτ。为了保证启动某体后，经nτ时间再次启动该体时，它的上次存取操作已完成，要求低位交叉存储器的模块数大于或等千n。以四体低位交叉编址的存储器为例，采用流水方式存取的示意图如图4.45所示。

可见，对千低位交叉的存储器，连续读取n个字所需的时间 t1 为t1 =T+(n-1)τ

若采用高位交叉编址，则连续读取 n个字所需的时间 t2 为 t2 =nT

打个比方，总线跑的快，他需要从多个体中取数据，之前总线是敲敲第一家门，等存储体把数据送出来，送到CPU后，还要到第一家送货一直等。

而现在，连续的数据在不同的家门，总线只需要挨家挨户敲门，等第一家开门后送第一家，回来的时候第二家已经开门了，就能实现持久的送货，提高效率。

高速缓冲存储器

在多体并行存储系统中，由于I/0设备向主存请求的级别高于 CPU访存，这就出现了 CPU等待 I/0 设备访存的现象，致使 CPU 空等一段时间，甚至可能等待几个主存周期，从而降低了CPU 的工作效率。为了避免 CPU 与 I/0 设备争抢访存，可在 CPU 与主存之间加一级缓存，这样，主存可将 CPU 要取的信息提前送至缓存，一旦主存在与 I/0 设备交换时，CPU 可直接从缓存中读取所需信息，不必空等而影响效率。这就是Cache的由来。

Cache

局部性原理

• 时间局部性：程序马上要用的数据可能就是现在正在频繁访问的数据
• 空间局部性：程序马上要用的信息很可能就是现在正在访问的数据周围的数据

Cache访问主存是按照块来搬运的，每次将一块的数据搬运到Cache中

Cache的工作原理

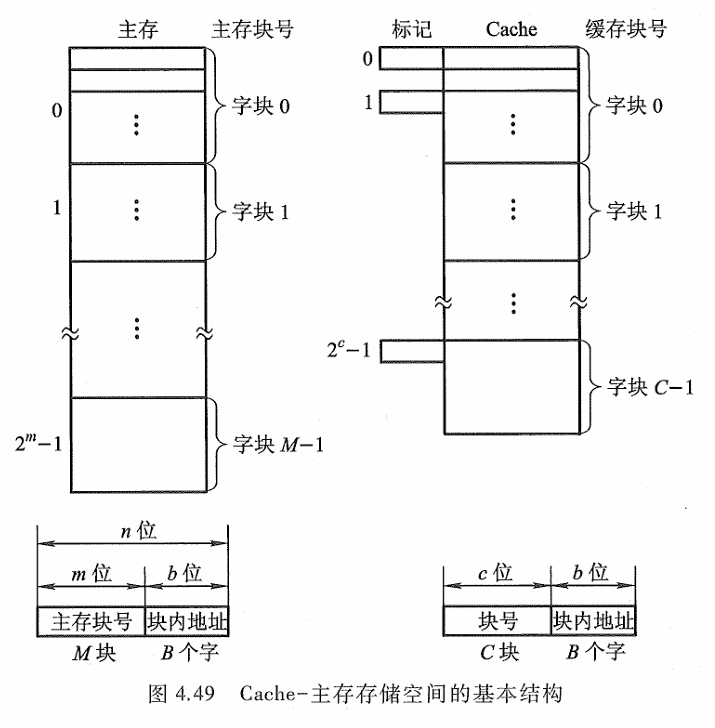
主存由 2n 个可编址的字组成，每个字有唯一的 n位地址。为了与 Cache 映射，将主存与缓存都分成若干块，每块内又包含若干个字，并使它们的块大小相同（即块内的字数相同)。这就将主存的地址分成两段：高m位表示主存的块地址，低b位表示块内地址，则 2^m=M表示主存的块数。

同样，缓存的地址也分为两段：高c位表示缓存的块号，低 b位表示块内地址，则 2^c= C表示缓存块数，且 C远小于M。主存与缓存地址中都用 b位表示其块内字数，即B=2^b 反映了块的大小，称B为块长。

任何时刻都有一些主存块处在缓存块中。 CPU 欲读取主存某字时，有两种可能：一种是所需要的字巳在缓存中，即可直接访问 Cache(CPU 与 Cache 之间通常一次传送一个字） ；另种是所需的字不在Cache 内，此时需将该字所在的主存整个字块一次调入 Cache 中(Cache 与主存之间是字块传送）。如果主存块已凋入缓存块，则称该主存块与缓存块建立了对应关系。

上述第一种情况为 CPU访问 Cache命中，第二种情况为 CPU访问 Cache 不命中。由于缓存的块数 C远小于主存的块数M，因此，一个缓存块不能唯一地、永久地只对应一个主存块，故每个缓存块需设一个标记 ，用来表示当前存放的是哪一个主存块，该标记的内容相当于主存块的编号。 CPU读信息时，要将主存地址的高 m 位（或 m位中的一部分）与缓存块的标记进行比较，以判断所读的信息是否已在缓存中。
Cache 的容量与块长是影响 Cache 效率的重要因素，通常用”命中率”来衡量 Cache 的效率。

在一个程序执行期间，设 $N_c$ 为访问 Cache 的总命中次数，$N_m$ 为访问主存的总次数，则命中率 $h$ 为

$$
h = \frac{N_c}{N_c + N_m}
$$

设 $t_c$ 为命中时的 Cache 访问时间，$t_m$ 为未命中时的主存访问时间，$1-h$ 表示未命中率，则 Cache-主存系统的平均访问时间 $t_a$ 为

$$
t_a = ht_c + (1-h)t_m
$$

当然，以较小的硬件代价使 Cache-主存系统的平均访问时间 $t_a$ 越接近于 $t_c$ 越好。用 $e$ 表示访问效率，则有

$$
e = \frac{t_c}{t_a} \times 100% = \frac{t_c}{ht_c + (1-h)t_m} \times 100%
$$

显然，h越接近1，访问效率越高