CS224-learn(2)

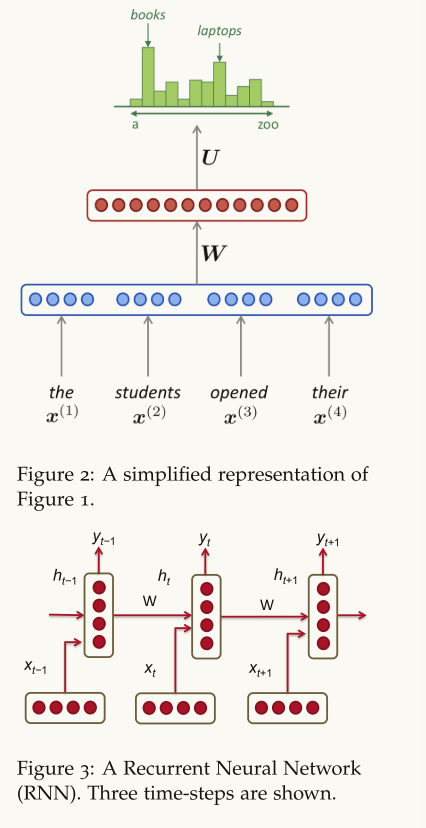
循环神经网络

  • 根据全部语料来调节模型
  • 单轮训练参数矩阵保持不变

$$
\begin{aligned}h_{t}&=\sigma(W^{(hh)}h_{t-1}+W^{(hx)}x_{[t]})\\hat{y}{t}&=softmax(W^{(S)}h{t})\end{aligned}
$$

RNN loss

$$
J^{(t)}(\theta)=-\sum_{j=1}^{|V|}y_{t,j}\times log(\hat{y}_{t,j})
$$

单个时间步的交叉熵损失

$$
J=\frac{1}{T}\sum_{t=1}^{T}J^{(t)}(\theta)=-\frac{1}{T}\sum_{t=1}^{T}\sum_{j=1}^{|V|}y_{t,j}\times log(\hat{y}_{t,j})
$$

整个语料库的平均交叉熵损失

$$
Perplexity=2^J
$$

困惑度

优缺点

  • 处理任意长度序列
  • 模型不会因为序列长度变长而变大
  • 使用了之前时间步的信息
  • 计算慢，无法并行
  • 梯度消失和爆炸

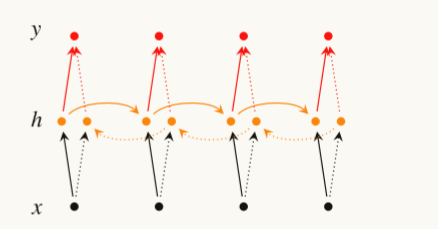
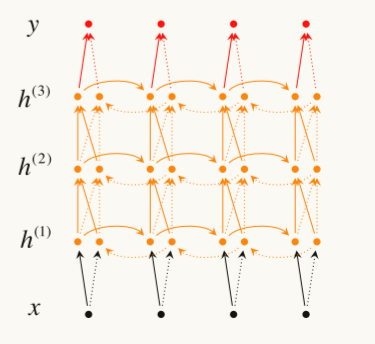
梯度双向RNN

img

同样也可以多层

使用简单的循环神经网络进行机器翻译的效果并不好，于是人们加入了几个优化

1745495633156

  • 使用两个不同的循环神经网络分别用于编码和解码
  • 使用三个输入来计算解码器的隐状态
  • 解码器前一个时间步的隐状态和预测值，编码器最后一个时间步的隐状态
  • 使用多层结构，需要更大的语料库
  • 使用双向循环神经网络
  • 反转输入单词的顺序来训练（）？

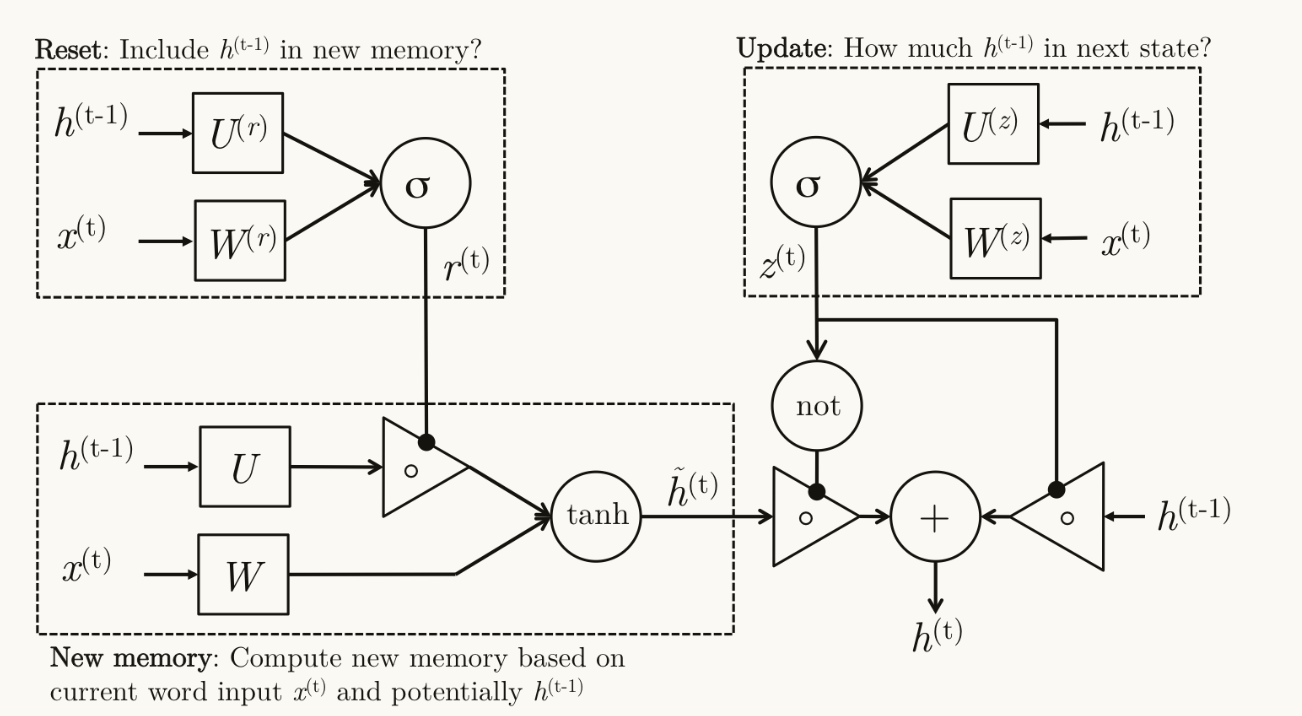
门控单元（GRU）

源于理论可以捕获长期以来关系，但实际表现不佳，所以采用门控单元实现更长久的记忆

$$
\begin{gathered}\mathrm{Z}{t}=\sigma(W^{(z)}x{t}+U^{(z)}h_{t-1})\text{(Update gate)}\\mathrm{r}t=\sigma(W^{(r)}x_{t}+U^{(r)}h_{t-1})\text{(Reset gate)}\\tilde{h}{t}=\tanh(r_t\circ Uh{t-1}+Wx_t)\mathrm{(New~memory)}\h_{t}=(1-z_t)\circ\tilde{h}t+z_t\circ h{t-1}\text{(Hidden state)}\end{gathered}
$$

  • 新记忆元：结合了重置门控制旧的隐状态参与更新的比例
  • 重置门：控制过去的隐状态在当前记忆元中的重要性
  • 更新门：用来控制有多少新的记忆元被转到下一个隐状态

这里更新门和重置门从公式上看好像都是在控制过去隐状态在当前状态的中的占比？

个人理解是更新门控制过去的历史消息在当前预测中的重要性即过去对当前影响重不重要，重置门用于用于决定过去的历史消息参不参与后续的运算，及时抛弃大概率没用了的记忆。

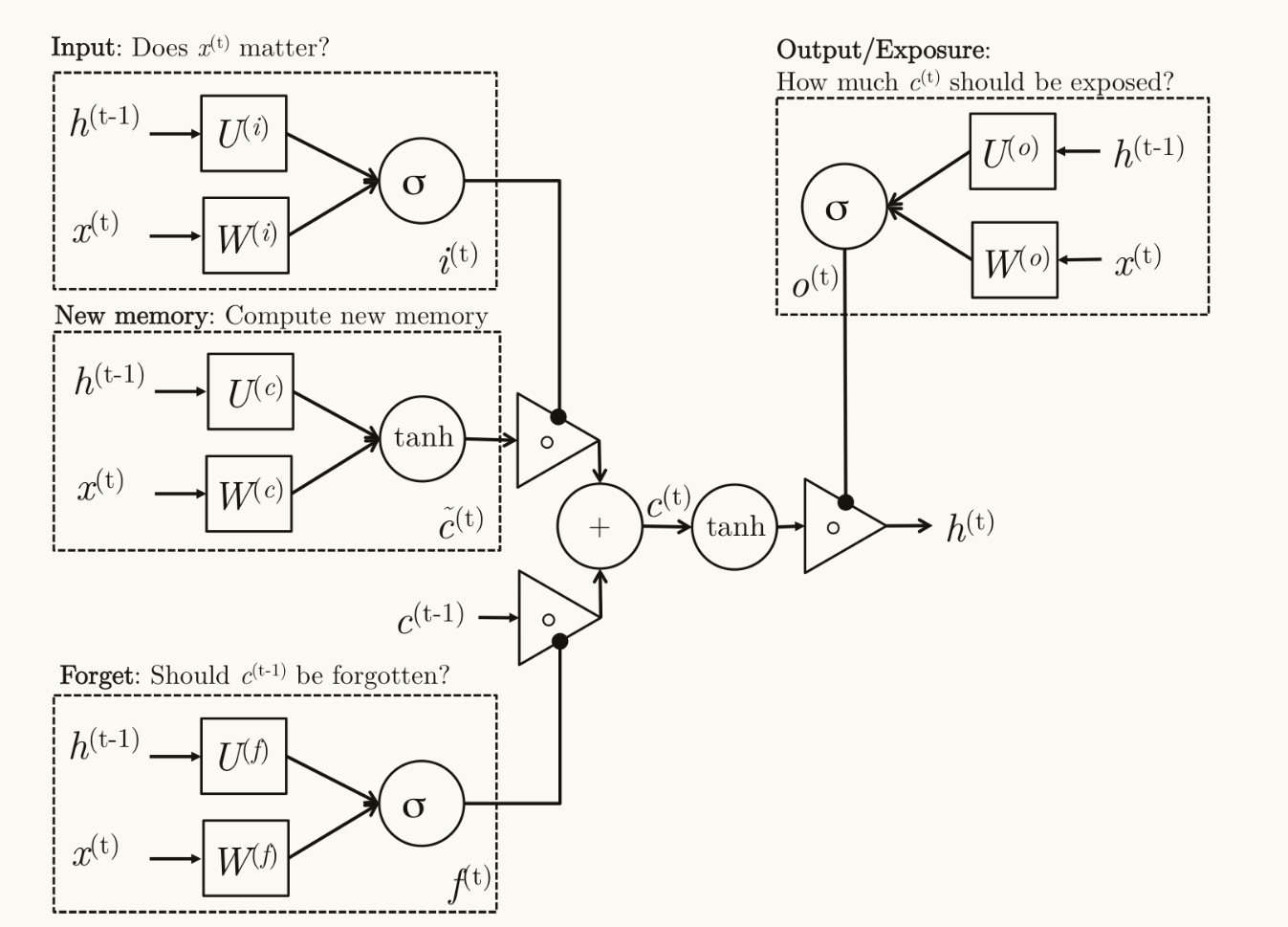
LSTM

比GRU更复杂一些的激活单元，但动机类似

$$
\begin{aligned}&\mathrm{i}t=\sigma(W^{(i)}x_{t}+U^{(i)}h_{t-1})&\text{(Input gate)}\&\mathrm{f}\dot{t}=\sigma(W^{(f)}x_{t}+U^{(f)}h_{t-1})&\text{(Forget gate)}\&\mathrm{o}t=\sigma(W^{(o)}x{t}+U^{(o)}h_{t-1})&\text{(Output/Exposure gate)}\&\tilde{c}t=\mathrm{tanh}(W^{(c)}x_{t}+U^{(c)}h_{t-1})&\text{(New memory cell)}\&c_{t}=f_t\circ c_{t-1}+i_t\circ\tilde{c}t&\text{(Final memory cell)}\&h{t}=o_t\circ\tanh(c_t)\end{aligned}
$$

在LSTM中，输入门，遗忘门，输出门的形式基本一致，但是享有不同的权重矩阵，在记忆元和隐状态的计算中，负责不同的部分。

新记忆元的组成分两部分，一方面接受遗忘门的建议，决定保留多少过去的记忆元，在这里输入门控制候选记忆的占有比例。

候选记忆在计算时不仅取决于当前状态的输入，还需要前一个时间步的隐状态，这并不与遗忘门控制过去记忆多余，而是候选记忆控制生成多少新记忆，而遗忘门控制保留多少旧记忆。

输出门较为特别，他们用于控制记忆有哪些信息需要保存到隐状态里。